
The traditional SAT (Paper) consists of 53 questions and 2 sections; No-Calculator and Calculator.
The Digital SAT, on the other hand, consists of a single part with 44 questions. However, the math topics in both exams are the same, meaning that the Digital SAT does not introduce new types of questions. Let’s get familiar with the math questions.
“SAT Math topics” are based on four main branches of mathematics:
- Numbers and Operations
- Algebra and Functions
- Geometry
- Data Analysis, Statistics, and Probability
Let’s review the types of questions from each topic.
Numbers and Operations

The question you see above is taken from the SAT exam booklet. To solve this question, the order should be:
Simplify the left side (opening the parentheses), keep the variable on the left side and move the integers to the right (6x = 42), then find X.
X = 7
Algebra and Functions
- Simplify linear and quadratic functions with exponents.
- Isolate the variable in a non-linear equation.
- Solve quadratic equations by factoring, completing the square, and using quadratic formulas.
- Perform operations with polynomial expressions.
- Solve equations that have variables in the denominator.
- Understand how the zeros and factors of a polynomial relate to each other and the graph.
- Understand how a non-linear graph relates to an equation or a system of equations.

In this question, g(4) means the value of x is 4. That is, if we substitute 4 for x in the inequality on the right side, the value of y will be 8. First, we need to find the value of a:
8 = 16a + 24
16a = -16; a = -1
Then after substituting the value of a, we need to substitute -4 for x and calculate:
g(-4) = (-1)(-4)(-4) + 24 = 8
Correct answer: A.
SAT Math Topics – Geometry
- Use area and volume formulas given on the test’s first page.
- Solve for missing information when parallel lines are intersected or in equilateral triangles.
- Solve right triangles using the Pythagorean theorem or trigonometric ratios.
- Use the relationship between similar triangles and trigonometric ratios.
- Calculate missing values in a circle (arc lengths, angle measures, chord lengths, sector areas).
- Convert between degrees and radians.
- Identify and interpret the standard form of a circle equation in the coordinate plane.
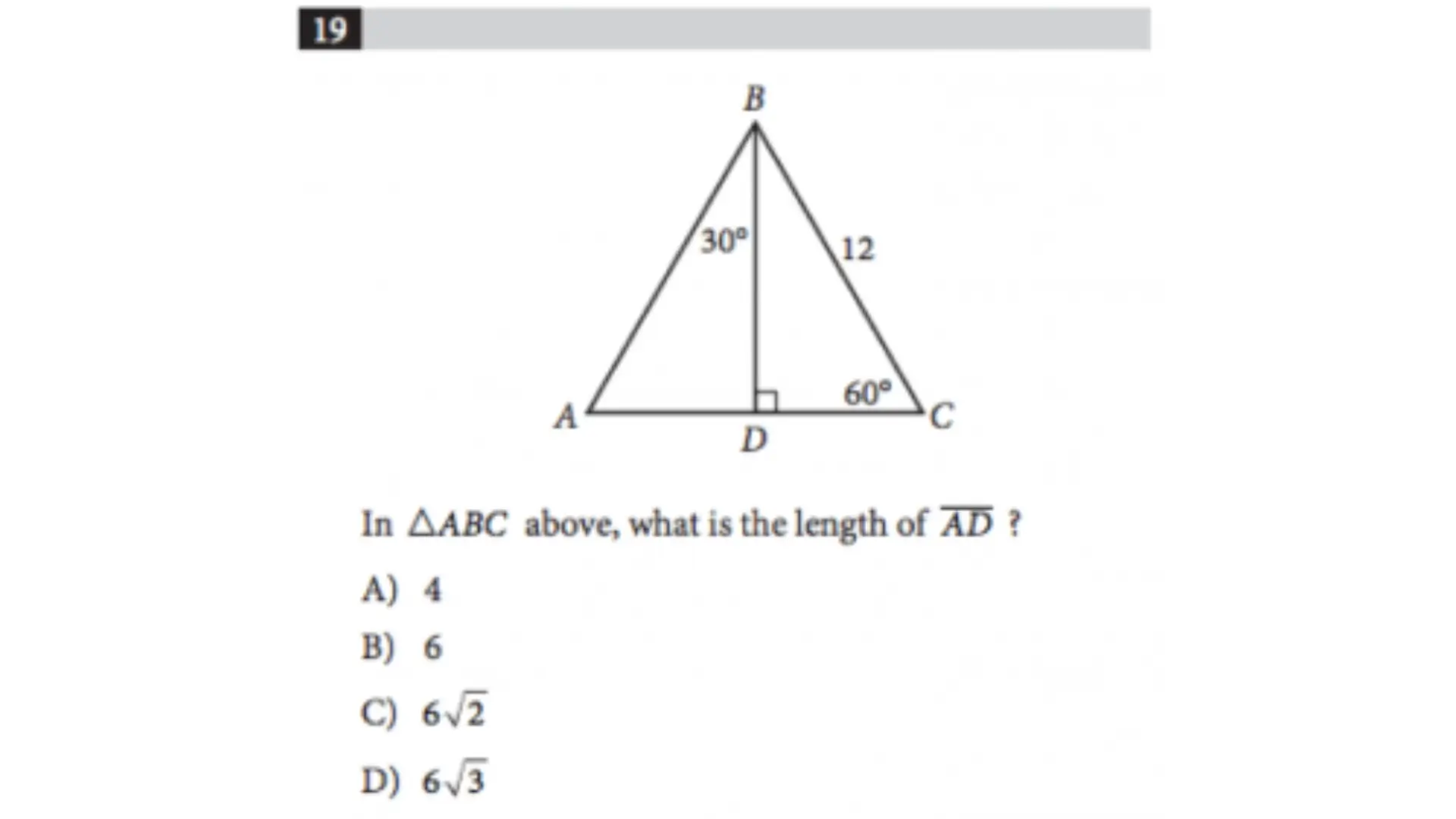
This question is relatively easy. First, we know that angle DBC is equal to 30. To solve, we can find the length of DC using trigonometric ratios. The side opposite a 30-degree angle is half of the hypotenuse. As you know, in an isosceles triangle, the height drawn from the top (BD) divides the base (AC) in half. That means AD and DC are equal.
Data Analysis, Statistics, and Probability
- Use ratios and percentages to solve problems.
- Perform unit conversions.
- Determine the best fit line or curve for a graph.
- Understand the difference between linear and exponential growth.
- Calculate probabilities.
- Calculate the mean, median, and range of data, and understand how these relate to the shape, center, and spread of data alongside standard deviation.
- Draw and justify statistical conclusions from data.

Let’s examine this question more closely. A table about dogs and cats is given. These are divided into two categories: those who eat only dry food and those who eat both dry and wet food. What is asked is the proportion of dogs that eat only dry food. The total number of dogs is 25. The number of dogs that eat only dry food is 2. The correct answer is B.




